142 Linked List Cycle II

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.
Note: Do not modify the linked list.

Solution

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if ( head == NULL or head->next == NULL ) return NULL;
        ListNode *p1 = head, *p2 = head->next;
        while ( p1 != p2 ) {
            p1 = p1->next;
            if ( p2->next == NULL ) return NULL;
            p2 = p2->next->next;
            if ( p2 == NULL ) return NULL;
        }
        p1 = head;
        p2 = p2->next;
        while ( p1 != p2 ) {
            p1 = p1->next;
            p2 = p2->next;
        }
        return p1;
    }
};

Thoughts
Step1: Detect whether there is a cycle in the linked list. Use two pointers, a fast one (p2) and a slow one (p1). Check whether they can meet before reaching the end of the linked list.

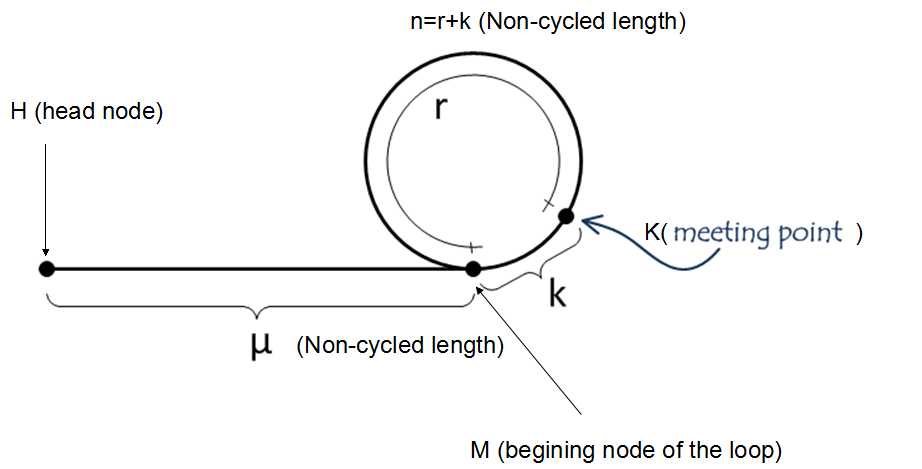
$$x=\mu+m(k+r)+k$$

$$2x=\mu+n(k+r) + k$$

$$\Rightarrow \mu+k = (n-2m)(k+r)$$

• $$(\mu+k)$$ is an integer multiple of $$(k+r)$$ (the length of the cycle). When $$(n-2m)=1$$, $$\mu+k = k+r$$, thus $$\mu = r$$.

Step2:
One pointer (p2) starts from the meeting point, and the other (p1) starts from the head.

• Let them traverse in the same speed, and will meet at the beginning node of the cycle.