207 Course Schedule
There are a total of n courses you have to take, labeled from 0 to n - 1.
Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1].
Given the total number of courses and a list of prerequisite pairs, is it possible for you to finish all courses?
For example:
2, [[1,0]]
There are a total of 2 courses to take. To take course 1 you should have finished course 0. So it is possible.
2, [[1,0],[0,1]]
There are a total of 2 courses to take. To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
Note: The input prerequisites is a graph represented by a list of edges, not adjacency matrices. Read more about how a graph is represented.
Hint
- This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses.
- Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort.
- Topological sort could also be done via BFS.
Solution
算法一:借鉴“逐层删去叶节点”的做法。
class Solution {
public:
bool canFinish(int numCourses, vector<pair<int, int>>& prerequisites) {
vector<int> pre(numCourses, 0);
vector<unordered_set<int>> graph(numCourses);
for ( auto e: prerequisites) {
if ( graph[e.first].find(e.second) == graph[e.first].end()) {
graph[e.first].insert(e.second);
pre[e.second] += 1;
}
}
for ( int remain = numCourses; remain >= 1; ) {
vector<int> level0;
int curr = remain;
for ( int i = 0; i <= numCourses-1; i++ ) {
if ( pre[i] == 0 ) {
pre[i] = -1;
level0.push_back(i);
remain -= 1;
}
}
if ( curr == remain ) return false;
for ( auto i: level0 ) {
for ( auto j: graph[i]) pre[j] -= 1;
}
}
return true;
}
};
modified 算法一
class Solution {
public:
bool canFinish(int numCourses, vector<pair<int, int>>& prerequisites) {
vector<int> pre(numCourses, 0);
vector<unordered_set<int>> graph(numCourses);
for ( auto e: prerequisites ) {
if ( graph[e.second].find(e.first) == graph[e.second].end() ) {
graph[e.second].insert(e.first);
pre[e.first] += 1;
}
}
vector<int> res;
int i = 0;
stack<int> s;
while ( s.size() != numCourses ) {
int i0 = i;
while ( pre[i] != 0 ) {
i = (i+1)%numCourses;
if ( i == i0 ) return false;
}
pre[i] = -1;
s.push(i);
for ( auto j : graph[i] ) pre[j] -= 1;
i = (i+1)%numCourses;
}
return true;
}
};
recursive 算法一
class Solution {
public:
bool helper(int numCourses, vector<unordered_set<int>>& graph, vector<int>& pre) {
if ( numCourses == 0 ) return true;
int i, n = pre.size();;
for ( i = 0; i <= n-1; i++ ) {
if ( pre[i] == 0 ) break;
}
if ( i == n ) return false;
pre[i] = -1;
for ( auto j: graph[i] ) pre[j] -= 1;
return helper(numCourses-1, graph, pre);
}
bool canFinish(int numCourses, vector<pair<int, int>>& prerequisites) {
vector<int> pre(numCourses, 0);
vector<unordered_set<int>> graph(numCourses);
for ( auto e: prerequisites ) {
if ( graph[e.second].find(e.first) == graph[e.second].end() ) {
graph[e.second].insert(e.first);
pre[e.first] += 1;
}
}
return helper(numCourses, graph, pre);
}
};
DFS
class Solution {
public:
bool canFinish(int numCourses, vector<pair<int, int>>& prerequisites) {
int n = prerequisites.size();
unordered_map<int, unordered_set<int>> graph;
for ( int i = 0; i <= n-1; i++ ) graph[prerequisites[i].first].insert(prerequisites[i].second);
while ( ! graph.empty() ) {
int start = graph.begin()->first;
unordered_set<int> s;
stack<int> path;
s.insert(start);
path.push(start);
while ( ! graph[start].empty() ) {
int end = *(graph[start].begin());
graph[start].erase(graph[start].find(end));
if ( graph[start].empty() ) graph.erase(graph.find(start));
if ( s.find(end) != s.end() ) return false;
s.insert(end);
path.push(end);
while ( ! path.empty() ) {
if ( graph.find(path.top()) == graph.end() ) {
s.erase(s.find(path.top()));
path.pop();
}
else {
start = path.top();
break;
}
}
if ( path.empty() ) break;
}
}
return true;
}
};
Notes
这是一道很好的图的题目,涉及很多基础算法。需要好好钻研加深理解。
- 算法一:首先考虑这道题本身,[n1, n2]表示上 n1 这门课之前需要上n2这门课(先修课)。用一个数组来计算每一门课的“先修”课程的数量。对于一个可行的课表,必定有至少一门课的“先修”课程数量为1。那么我们就先上这样的课(定义为level0的课)。把level0的课上完之后,对依赖于level0的所有课程的“先修”课程数量进行调整(减1)。这样问题规模缩小,但可以用同样算法解决。
- 当不再存在level0的课程,而剩下的课程数非0时,表明不存在可行的安排;
- 当问题可以缩小到课程数为0的时候,表明存在可行的安排。 这个算法的优点在于在判断是否可行的同时,也提供了一种如何找到一种合理课程安排的方法。(即总是先上level0的课)
这个算法其实就是利用Kahn算法进行拓扑排序(topological sort)。事实上,不需要逐层删除。每当删除一门“先修课程”为零的课程,我们对pre数组作相应调整,找到下一个“先修课程”为零的课程即可。这样代码会更简洁(modified算法一)。该算法也可以写成recursive的形式(recursive算法一)。
算法二: 拓扑排序也可以通过DFS实现。
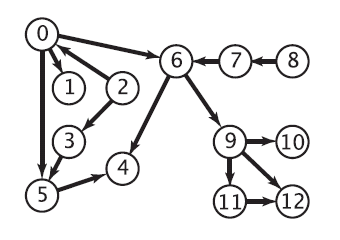
对于如上有向图,求一条路径使得对任意边(u,v)都有u在路径中先于v出现。- 则对于出度为0的边,我们总想优先访问。(这是Kahn算法的思想。)
- 对于入度为0的边,如2,在访问2之前必须先访问0和3。由此我们可以递归地遍历整个图。只有当以该顶点为起点的边对应的终点都访问过了,我们才可以把该顶点添加到访问路径中。
来看一下python代码,这里除了判断环的存在,也输出了访问路径。
def visit(i, graph2, visited, sub_path, path):
if ( i in sub_path ): return False
if ( i in visited ): return True
visited.append(i)
sub_path.append(i)
for j in graph2[i]:
if (not visit(j, graph2, visited, sub_path, path)): return False
sub_path.pop()
path.append(i)
return True
def dfs(n, outdegree, graph2):
visited = []
sub_path = []
path = []
for i in range(n):
if ( outdegree[i] != 0 ): continue
if ( not visit(i, graph2, visited, sub_path, path) ): return []
return path
- 这里用一个sub-path来记录当前扫描的路径,用于检测是否存在环。(注意
in visited和in sub-path是两种不同的条件。) - 在处理DFS的问题中,经常不确定如何恢复path,要特别注意一下。
- 这里用一个sub-path来记录当前扫描的路径,用于检测是否存在环。(注意